PianoCarriera
Dans ce challenge, je dois aider un élève à « trafiquer » le site d’inscription de son université pour l’inscrire à un cours (internship) auquel il n’est pas sensé avoir accès
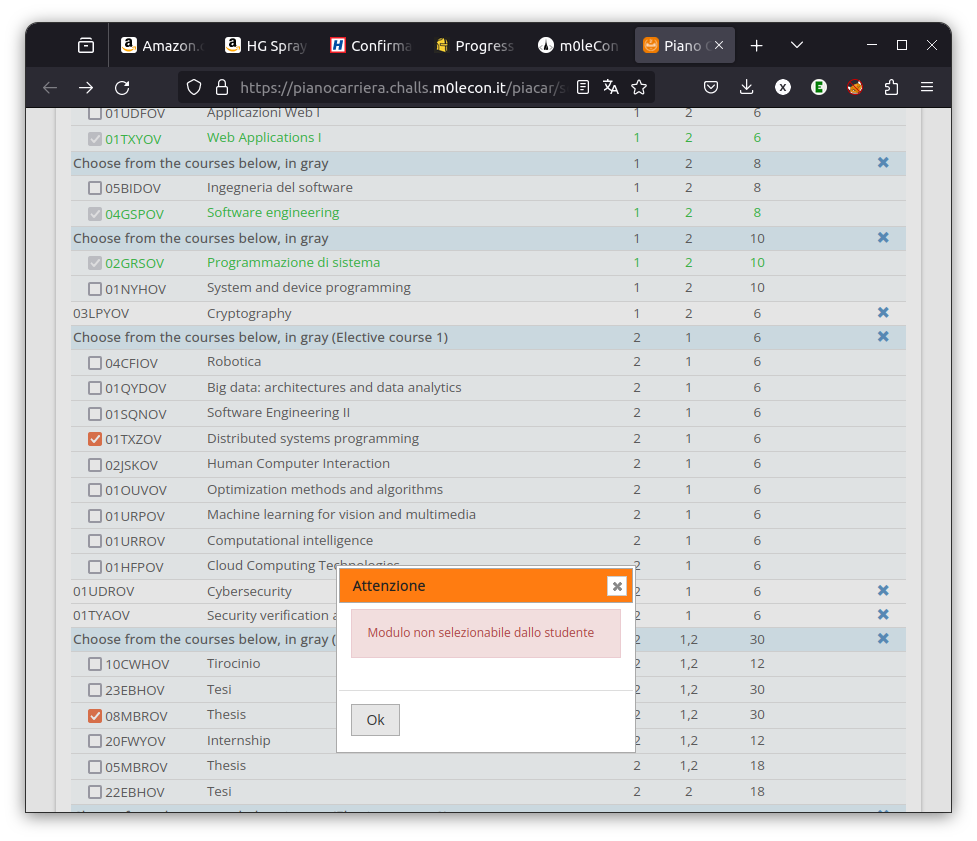
Comme d’habitude, une petite plongée dans le code permet de comprendre ce qu’il se passe. Un passage attire mon attention:
if($(this).hasClass('noProp')){
checkbox.attr('checked',false);
$( "#msg2" ).empty();
var myMsg='<div class="alert alert-danger">Modulo non selezionabile dallo studente</div>';
$( "#msg2" ).append(myMsg);
$( "#msg2" ).dialog({
maxWidth:600,
maxHeight: 300,
modal: true,
autoOpen: true,
buttons: {
"Ok": function() {
$( this ).dialog( "close" );
$( "#msg2" ).empty();
}
}
});
}Apparemment, le code se base sur la présence de la classe noProp dans la balise de la case à cocher. Qu’à cela ne tienne, je vais juste utiliser les « dev tools » de mon navigateur pour retirer la classe noProp de l’élément! Après quelques essais, il semble que je doive avoir un total de 30 crédits dans la catégorie. Pas de soucis, j’ajoute un deuxième cours à 18 crédits de la même façon, et j’obtiens le flag!
PoliTO ch(e)atbot
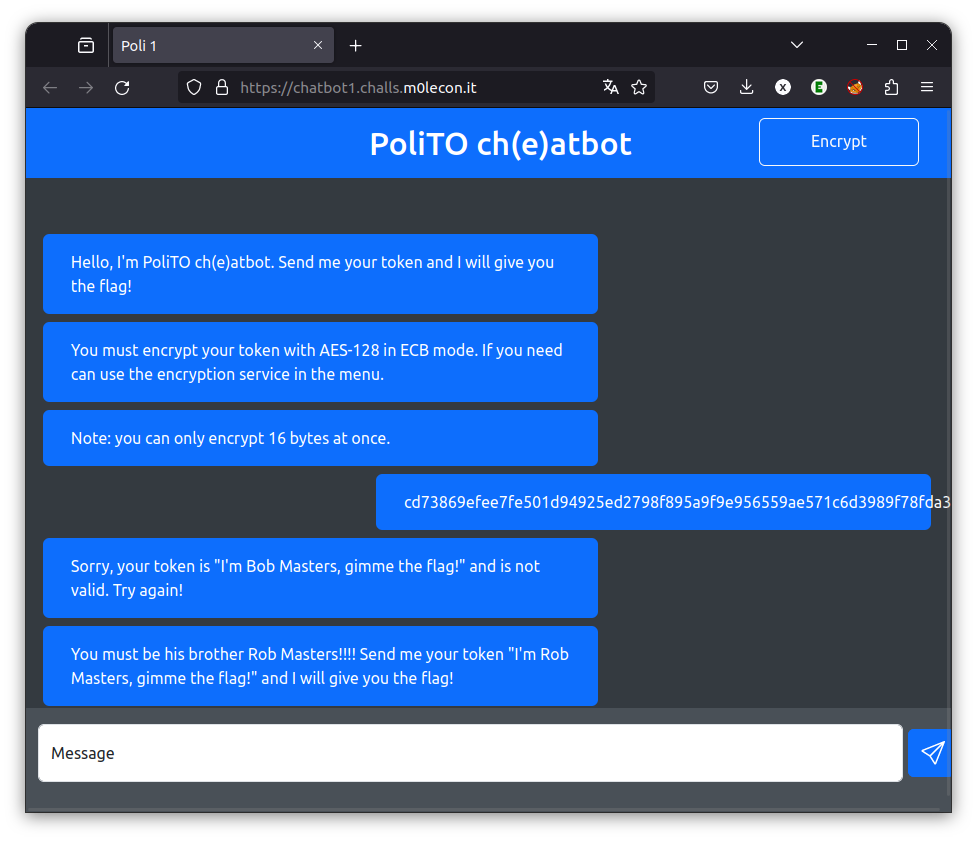
Dans ce challenge, je dois crypter une phrase donnée et l’envoyer au chatbot pour recevoir le flag. Je dispose d’un outil pour crypter un message, mais ce message est limité à 16 caractères (or le message que je dois envoyer en compte plus de 16)
Je dispose également du résultat du cryptage d’une chaine qui est presque le message que je dois crypter
Le cryptage est AES-218 en mode ECB (Electronic Code Book). Voilà la faille que je vais exploiter. En effet, la particularité du mode ECB est que chaque bloc du message (16 bytes dans notre cas) est encodé de manière totalement indépendante. Je peux donc crypter 16 caractères correspondant au bon message, puis compléter avec le reste du message crypté
| I’m Bob Masters, | gimme the flag! |
| cd73869efee7fe501d94925ed2798f89 | 5a9f9e956559ae571c6d3989f78fda3c |
| I’m Rob Masters, | |
| 1be39bf6015076ba70446ca402584e98 |
La deuxième ligne du tableau est le message crypté affiché dans le chat
La quatrième ligne est le résultat du cryptage de « I’m Rob Masters, » via l’outil fourni
Il suffi alors de combiner les deux parties pour obtenir le bon message crypté
1be39bf6015076ba70446ca402584e985a9f9e956559ae571c6d3989f78fda3c
Et voilà, le c’est gagné!
PoliTO ch(e)atbot 2.0
Cette fois, le chatbot propose un challenge un peu différent
un OTP (one time pad) est une technique de cryptage totalement sécurisée. Il est impossible de décrypter le message sans la clef.
Le principe de l’OTP est simple: le message est XORé avec une clef aussi longue que le message, formée de bytes aléatoires.
Le problème, c’est que, comme on peut le constater en utilisant l’outil fourni, on est très très loin d’un OTP
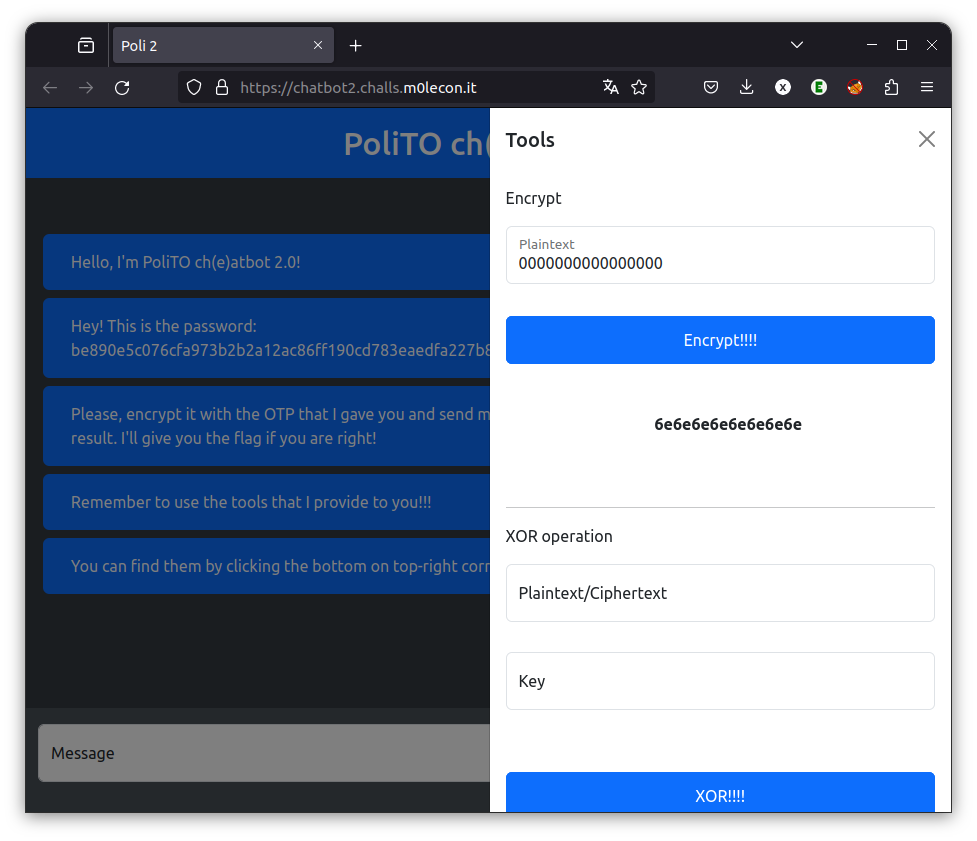
Visiblement, la clef générée ne fait qu’un seul byte, qui est répété autant de fois que nécessaire pour avoir une clef aussi longue que le message.
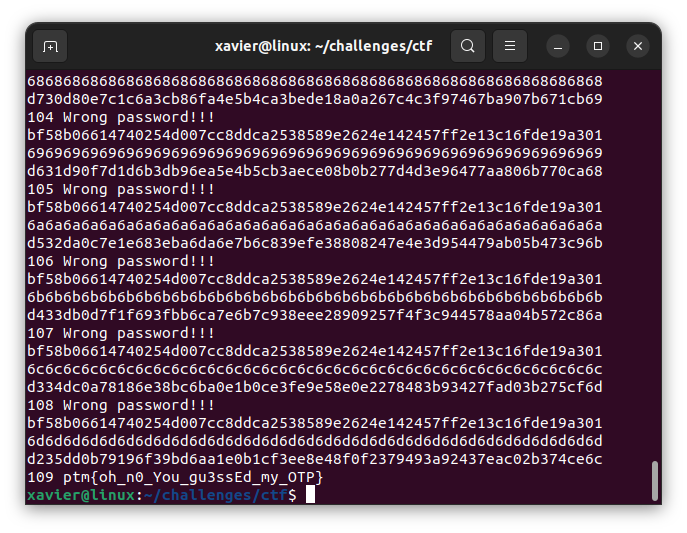
Au lieu d’avoir un nombre astronomiques de clefs possibles, on en a seulement 256, suffisamment pour un leger bruteforce:
import requests
from time import sleep
c="bf58b06614740254d007cc8ddca2538589e2624e142457ff2e13c16fde19a301"
url="https://chatbot2.challs.m0lecon.it/api/v1/message"
for i in range(1,256):
k=f"{i:02x}"*(len(c)//2)
print(c)
print(k)
p=hex(int(c,16)^int(k,16))[2:]
if len(p)%2!=0:p="0"+p
print(p)
resp=requests.post(url,json={"message":p},cookies={"session":"xxxxxxxx-xxxx-xxxx-xxxx-xxxxxxxxxxxx"}).json()["message"]
print(i,resp)
if resp!="Wrong password!!!":
exit()
sleep(0.5) # so I don't overload the server...
Après une petite attente, le flag est capturé!