Récit d’un CTF (partie 2)

SecureAccess

L’objectif de ce challenge est de s’enregistrer comme un user « admin »

Nous disposons de deux choses:

• le site web
• un fichier .pyc

Le site web permet d’enregistrer un utilisateur. Le processus d’enregistrement demande de fournir un token.

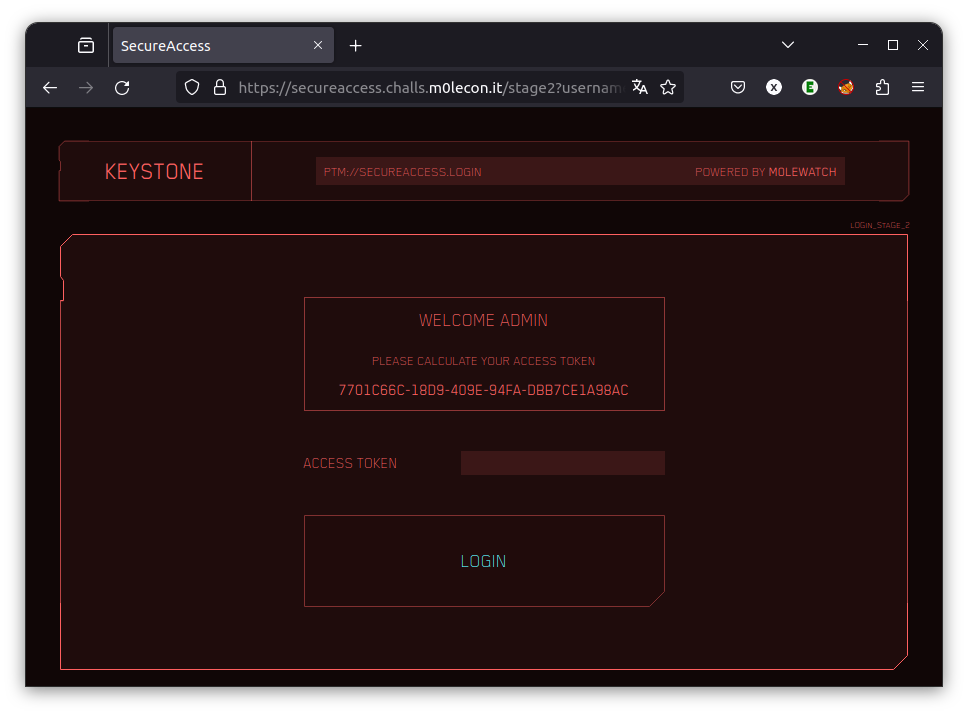
Le fichier .pyc est un fichier python compilé. Il existe une multitude d’outils permettant de décompiler un pyc pour retrouver le code source. J’ai opté pour un décompilateur online, qui m’a fourni la source suivante:

# uncompyle6 version 3.5.0
# Python bytecode 3.8 (3413)
# Decompiled from: Python 2.7.5 (default, Jun 20 2023, 11:36:40) 
# [GCC 4.8.5 20150623 (Red Hat 4.8.5-44)]
# Embedded file name: leaked.py
# Size of source mod 2**32: 304 bytes
import hashlib, json, base64

def generate_token(nonce: str):
    username = 'user'
    secret = hashlib.sha256(username.encode() + nonce.encode()).hexdigest()
    bundle = {'user':username, 
     'secret':secret}
    return base64.b64encode(json.dumps(bundle).encode())

Il s’agit vraisemblablement de la fonction qui permet de générer le token demandé.

Une petite modification du code, et j’obtiens le token qui me donne accès au flag!

import hashlib, json, base64

def generate_token(nonce: str):
    # /!\ change the user to admin
    username = 'admin'
    secret = hashlib.sha256(username.encode() + nonce.encode()).hexdigest()
    bundle = {'user':username, 
     'secret':secret}
    return base64.b64encode(json.dumps(bundle).encode())

# calling the function with the nonce given by the website
print(generate_token("7701C66C-18D9-409E-94FA-DBB7CE1A98AC"))

Fast RSA

Cette fois, le flag est crypté avec l’algorithme RSA. La sécurité de cet algorithme est mathématiquement prouvée. Néanmoins, certaines implémentations (comme celle-ci) comportent des failles qui permettent à un attaquant de cracker le cryptage.

from Crypto.Util.number import getPrime, isPrime, bytes_to_long
from secret import flag

flag = bytes_to_long(flag)

def GeneratePublicKey():
    while True:
        p = getPrime(512)
        q = p + 4
        if isPrime(q):
            return (p, q)

p, q = GeneratePublicKey()
n = p*q
e = 65537
d = pow(e, -1, (p-1)*(q-1))

ciphertext = pow(flag, e, n)

print(n)
print(e)
print(ciphertext)

# OUTPUT    
# n = 73835355773586632749497813712844974279688700968581353676365718256887741429589293987167857318819304298761226530765222129869744268663458302484923609419850715086294772630316875879671931990860760168632405376915473464245173555210859733420012801323450300287286827847372572895767079204521003431182215766356958645741
# e = 65537
# ciphertext = 69088718730225565550533207665423162086878540640610709978042785622785990794595484186604907117720523080139401746613418389574889276052615162202284720710353059616183359504400646419053826554396432853908827511966214885915759786569544232364425295062591653836236590708223539383404510598672913303248612361154693570128

Dans ce cas, la faille est dans la génération des deux nombres premiers p et q. Normalement, ces deux nombres premiers sont totalement indépendants, ce qui rend la factorisation de N presque impossible. Mais ici on sait que q=p+4.

il suffit donc de trouver un nombre p tel que p*q=p*(p+4)=n. Cela revient à une simple équation du second degré, avec de très très grands nombres

p² + 4p - n = 0
==> rho=16+4*n
==> p=(-4+-sqrt(rho))/2=-2+-sqrt(4+n)

Cela semblait pourtant une bonne idée, mais cela ne donne aucun résultat.

J’ai donc essayé une autre approche, en supposant que p et q sont proches, donc proches de la racine carrée de N.

from Crypto.Util.number import long_to_bytes
 
n = 73835355773586632749497813712844974279688700968581353676365718256887741429589293987167857318819304298761226530765222129869744268663458302484923609419850715086294772630316875879671931990860760168632405376915473464245173555210859733420012801323450300287286827847372572895767079204521003431182215766356958645741
e = 65537
ciphertext = 69088718730225565550533207665423162086878540640610709978042785622785990794595484186604907117720523080139401746613418389574889276052615162202284720710353059616183359504400646419053826554396432853908827511966214885915759786569544232364425295062591653836236590708223539383404510598672913303248612361154693570128

def bigSqrt(x):
	mininc=1
	maxexc=x
	while maxexc-mininc>1:
		pivot=(mininc+maxexc)//2
		p2=pivot**2
		if p2==x:	return pivot
		elif p2>x:	maxexc=pivot
		else:		mininc=pivot+1
	print ("check",mininc**2-x)
	return mininc

z=bigSqrt(n)
for i in range(z-1000,z+1000):
	if n%i==0: 
		p=i
		q=n//i
		print(p)
		print(q)
		print("check",n-p*q)
		d=pow(e, -1, (p-1)*(q-1))
		plain=long_to_bytes(pow(ciphertext,d,n))
		print(plain)

Et voilà, le flag est obtenu! En réalité, les q=p+100 et non p+4…